The current industry protocol for durability testing of vascular stents and frames involves testing many implants simultaneously at a range of different stimulus magnitudes (typically strain or stress). The test levels are spread out like a grid across the stimulus range of interest. Each implant is tested to failure or run-out at its specified level and a model is fit to the data using methods similar to those described in Meeker and Escobar.1 An example of a completed durability test of this type is shown below.2 Of interest to the designer is the distribution of stimulus levels that would be expected to cause a failure at a specified cycle count like 400 million.
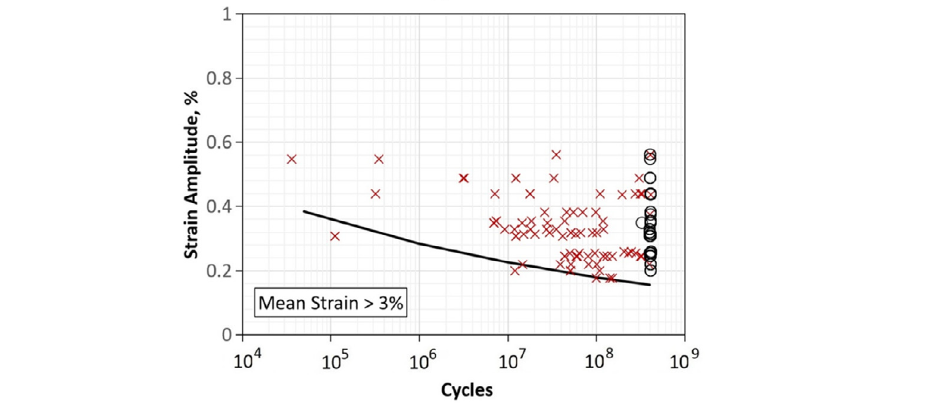
This methodology works well if you have a large budget and is accepted by FDA. However, blanketing the parameter space with enough samples to fit a robust model can be very costly and requires enough lab equipment to do many tests in parallel. I recently learned that there is another way that has the potential to significantly reduce test burden and allows for some unique advantages. I will attempt to describe it below.
Sensitivity testing represents a different paradigm in which samples are tested sequentially rather than in parallel. In such testing, the outcome of the first test informs the stimulus level of the second test and so on. When an implant fails at a given stimulus, the next part is tested at a lower level. When it passes, the stimulus on the next is increased. In this way, the latent distribution of part strength is converged upon with each additional test providing improved precision.
The key questions that must be answered to execute a sequential sensitivity test:
- “How to specify the test levels for subsequent runs in a principled and efficient way?”
- “How to estimate the underlying failure strength distribution when the threshold for failure is not directly assessed on each run?”
Neyer was the first to present a D-Optimal answer to the first question.3 Implementation of the algorithm for determining sequential levels that minimize the test burden and converge on the true underlying strength distribution quickly is not trivial and historically has remained unavailable outside of pricey commercial software.4 Fortunately, generous and diligent researchers have recently created an open source tool in R called “gonogo” which can execute sequential testing according to the D-optimal Neyer algorithm (or its improved direct descendants).5
In the remainder of this post I will show how to use gonogo to determine the underlying strength distribution of hypothetical vascular implant and visualize uncertainty about the estimate.
- Load Libraries
- Accessing gonogo Functions
- Simulating A Sequential Sensitivity Experiment
- Confidence, Reliability, and Visualization
- Conclusion and Thanks
- Session Info
Load Libraries
library(tidyverse)
library(gt)
library(plotly)
library(ggrepel)
library(here)
library(gonogo)
library(ggalt)Accessing gonogo Functions
The functions in gonogo can be accessed in 2 ways:
I will be using the code sourced from Jeff’s site as the functions are more readily editable.
source(here("gonogoRiley.R"))Simulating A Sequential Sensitivity Experiment
There are some nice built-in simulation features in gonogo using the gonogoSim function. For our walkthrough though we’ll simulate the data manually to have better visibility of what’s happening under the hood.
Suppose we have a part budget of n=25 stents from manufacturing and our goal is to estimate the underlying distribution of stress amplitude that causes fatigue fracture. First, let’s simulate the failure strength of the 25 parts using a known distribution (which is only available in the simulation). We’ll assume failure stress amplitude for these parts is normally distributed with a mean of 600 MPa and standard deviation of 13 MPa.
Simulate the Strength of Each Part
set.seed(805)
stent_strength_tbl <- tibble(part_strength_mpa = rnorm(n = 25, mean = 600, sd = 13))
stent_strength_tbl %>%
gt_preview()| part_strength_mpa | |
|---|---|
| 1 | 602.0110 |
| 2 | 585.2761 |
| 3 | 603.3943 |
| 4 | 569.8526 |
| 5 | 601.5328 |
| 6..24 | |
| 25 | 600.9657 |
See Test Levels and Input Test Results
The gonogo() function will initiate the test plan for sequential testing that prescribes test levels based on the outcome of each run. This operation happens in the console as shown in the screenshot below.
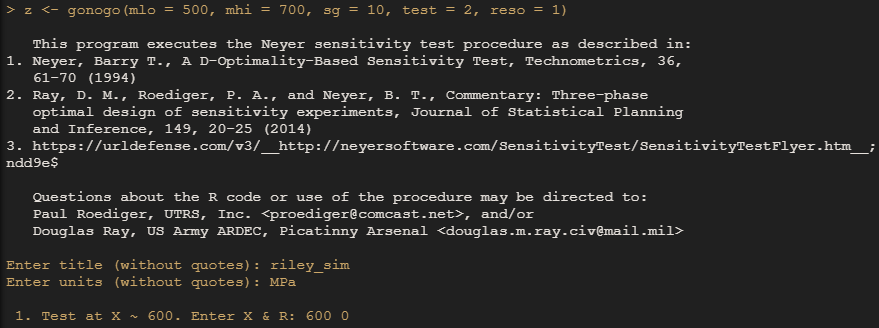
We’ll use the Neyer option by setting the “test” argument equal to 2. One key feature of sequential testing is that high and low initial guesses for the mean must be provided at the onset of testing along with an initial guess for the standard deviation. These guesses help set the scale. We’ll provide vague guesses that would be reasonable given our domain knowledge of cobalt-based alloys and their fatigue properties.
If we were really running the test on physical parts we’d want to set up a test at the prescribed stimulus level, then report the result to the console by inputing 2 numbers: the level you actually ran the test at (should be the same as what was recommended) and the outcome (1 for failure or 0 for survival) separated by a single space. After the results from the first test are entered, the recommended level of the next test is presented. When all runs are complete, the results are stored in the assigned object.
# z <- gonogo(mlo = 500, mhi = 700, sg = 10, test = 2, reso = 1) #input results in consoleThe resulting object z is a list that has a lot of information. The following code will pull the run history and clean it up nicely with tools and formatting from gt package.
z$d0 %>%
gt() %>%
cols_align("center") %>%
opt_row_striping(row_striping = TRUE) %>%
tab_header(
title = "Run History of Sensitivity Test of n=25 Stents",
subtitle = "X and EX are Stimulus Levels, Y = Outcome (1 = part failed, 0 = part survived)"
) %>%
cols_width(everything() ~ px(100)) %>%
tab_style(
style = list(
cell_text(weight = "bold")
),
locations = cells_column_labels(columns = everything())
)| Run History of Sensitivity Test of n=25 Stents | ||||||
|---|---|---|---|---|---|---|
| X and EX are Stimulus Levels, Y = Outcome (1 = part failed, 0 = part survived) | ||||||
| X | Y | COUNT | RX | EX | TX | ID |
| 600 | 0 | 1 | 600 | 600.0000 | 600 | B0 |
| 650 | 1 | 1 | 650 | 650.0000 | 650 | B1 |
| 625 | 1 | 1 | 625 | 625.0000 | 625 | B3 |
| 612 | 1 | 1 | 612 | 612.5000 | 612 | B3 |
| 606 | 1 | 1 | 606 | 606.0000 | 606 | B3 |
| 590 | 0 | 1 | 590 | 589.7220 | 590 | B4 |
| 593 | 0 | 1 | 593 | 592.5733 | 593 | B4 |
| 611 | 0 | 1 | 611 | 610.7146 | 611 | B4 |
| 617 | 1 | 1 | 617 | 616.8731 | 617 | II1 |
| 599 | 1 | 1 | 599 | 599.4648 | 599 | II2 |
| 590 | 0 | 1 | 590 | 590.4793 | 590 | II2 |
| 616 | 1 | 1 | 616 | 615.7384 | 616 | II2 |
| 593 | 1 | 1 | 593 | 592.9877 | 593 | II2 |
| 584 | 0 | 1 | 584 | 583.6982 | 584 | II2 |
| 585 | 0 | 1 | 585 | 585.3147 | 585 | II2 |
| 615 | 1 | 1 | 615 | 615.2118 | 615 | II2 |
| 587 | 0 | 1 | 587 | 587.4391 | 587 | II2 |
| 613 | 1 | 1 | 613 | 613.3351 | 613 | II2 |
| 612 | 1 | 1 | 612 | 612.3336 | 612 | II2 |
| 589 | 0 | 1 | 589 | 589.3771 | 589 | II2 |
| 611 | 1 | 1 | 611 | 611.0667 | 611 | II2 |
| 590 | 0 | 1 | 590 | 590.4844 | 590 | II2 |
| 610 | 1 | 1 | 610 | 610.0713 | 610 | II2 |
| 591 | 0 | 1 | 591 | 591.3679 | 591 | II2 |
| 609 | 1 | 1 | 609 | 609.2816 | 609 | II2 |
Gonogo has some really convenient built-in visualization tools. The run history can be plotted using gonogo’s ptest function with argument plt=1.
ptest(z, plt = 1)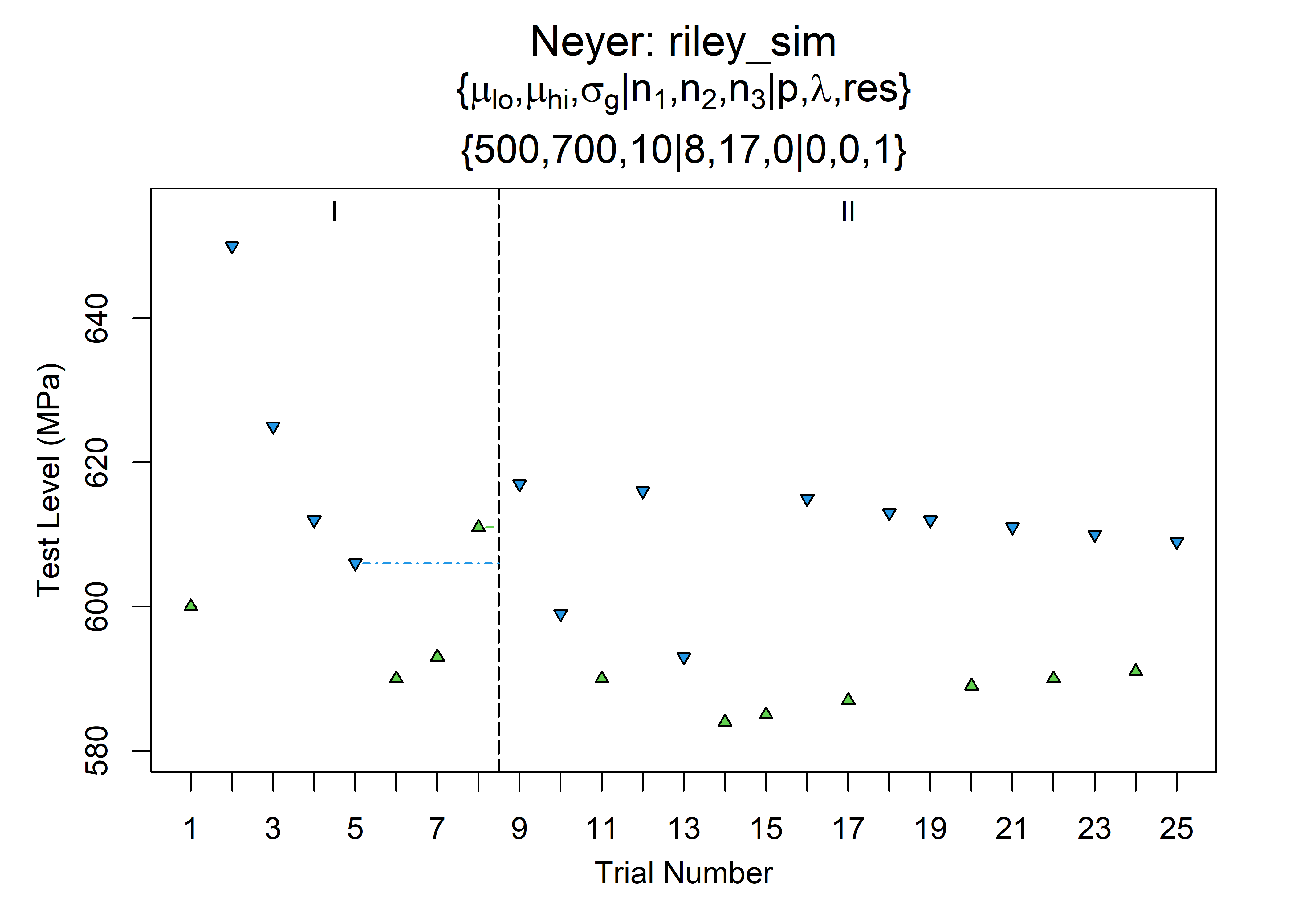
## NULLThe values we really care about are the estimates of the mean and sd of the latent failure strength distribution. Numerical MLE’s for these parameters can be quickly extracted as follows:
z$musig## [1] 600.383131 7.894673We see that these are quite close to the true parameters of mean = 600 MPa, sd = 13 MPa! That really impressive for only 25 parts and vague initial guesses.
I like to occasionally look under the hood and see how the outputs are generated. I don’t always understand it but it helps me learn. In this case, the calculations to extract an estimate are pretty simple. gonogo is using a glm with probit link function. The results are replicated here with manual calculations.
xglm <- glm(Y ~ X, family = binomial(link = probit), data = z$d0)
ab <- as.vector(xglm$coef)
muhat <- -ab[1] / ab[2]
sighat <- 1 / ab[2]
tibble(
true_parameter = c(600, 13),
gonogo_estimate = c(muhat, sighat)
) %>%
mutate(gonogo_estimate = gonogo_estimate %>% round(1)) %>%
gt()| true_parameter | gonogo_estimate |
|---|---|
| 600 | 600.4 |
| 13 | 7.9 |
Confidence, Reliability, and Visualization
We just identified the MLE’s for the latent strength distribution. But anytime we’re working with medical devices we have to be conservative and respect the uncertainty in our methods. We don’t want to use the mean of the distribution to describe a design. Instead, we identify a lower quantile of interest and then put a confidence interval on that to be extra conservative.6 gonogo has some great tools and functions for helping us achieve these goals. I prefer to use the tidyverse framework for my data analysis and visualization so I combine the built in functions from gonogo with some helper functions that I wrote to keep things tidy. I present them here with some description of what they do but not much explanation of how they work. Sorry.
I will note however that gonogo provides options for obtaining multiple forms of confidence intervals: Fisher Matrix, GLM, and Likelihood-Based. For additional information on how it calculates each type, refer to THIS DOCUMENTATION. In the tests I ran, GLM and LR based CIs performed almost the same; FM was different. I use GLM below for my purposes.
In the following work, I assume we care about the 95% confidence bound on the .10 quantile. gonogo calculates all intervals as 2-sided, so to get the 95% confidence bound (1-sided) we request the 90% 2-sided limits.
Extract a tibble of 2-sided, pointwise confidence limits about all quantiles
This first function takes the output from the gonogo function and calculates 2-sided .90 confidence bounds on the various quantiles. The lims() function is from gonogo.
# helper function
conf_limits_fcn <- function(tbl, conf = .9) {
conf_limits_tbl_full <- lims(ctyp = 2, dat = tbl, conf = conf, P = seq(from = .01, to = .99, by = .01)) %>%
as_tibble() %>%
rename(
ciq_lower = V1,
estimate_q = V2,
ciq_upper = V3,
ip_lower = V4,
estimate_p = V5,
cip_upper = V6
)
}
rileysim_conf_tbl <- conf_limits_fcn(z$d0)
rileysim_conf_tbl %>%
gt_preview()| ciq_lower | estimate_q | ciq_upper | ip_lower | estimate_p | cip_upper | |
|---|---|---|---|---|---|---|
| 1 | 566.0095 | 582.0174 | 590.1744 | 0.000057 | 0.01 | 0.127107 |
| 2 | 569.7538 | 584.1695 | 591.6789 | 0.000283 | 0.02 | 0.165152 |
| 3 | 572.1145 | 585.5349 | 592.6478 | 0.000714 | 0.03 | 0.193273 |
| 4 | 573.8819 | 586.5620 | 593.3851 | 0.001369 | 0.04 | 0.216580 |
| 5 | 575.3128 | 587.3975 | 593.9914 | 0.002260 | 0.05 | 0.236954 |
| 6..98 | ||||||
| 99 | 610.9205 | 618.7489 | 633.9138 | 0.884141 | 0.99 | 0.999923 |
Extract a point estimate for the lower 2-sided confidence limit for the .10 quantile.
We present results to FDA using the terminology “confidence and reliability”. By extracting the lower end of the 2-sided 90% confidence band on the .10 quantile, we obtain an estimate of the 95/90 tolerance bound i.e. a bound above which we would expect 90% or more of the population to lie, with 95% confidence. This would be a conservative estimate of the endurance limit for this stent design.
lower_conf_fcn <- function(tbl, percentile) {
lower_scalar <- tbl %>%
mutate(qprobs = qnorm(estimate_p)) %>%
arrange(qprobs) %>%
filter(estimate_p == percentile) %>%
mutate(ciq_lower = ciq_lower %>% round(1)) %>%
pluck(1)
lower_qnorm <- tbl %>%
mutate(qprobs = qnorm(estimate_p)) %>%
arrange(qprobs) %>%
filter(estimate_p == percentile) %>%
pluck(7)
lower_tbl <- tibble(
estimate_q = lower_scalar,
estimate_p = percentile,
qprobs = lower_qnorm
)
return(lower_tbl)
}
lower_conf_fcn(rileysim_conf_tbl, percentile = .1) %>% pluck(1)## [1] 580.2Plot CDF
Now some plotting functions to help visualize things. First, we use our confidence limit dataframe from above to construct a cdf of failure strength. With some clever use of geom_label_repel() and str_glue() we can embed our data right onto the plot for easy communication. The estimated endurance limit from our test sequence is 580 MPa.
plot_cdf_fcn <- function(tbl, percentile = .1, units = "MPa") {
tbl %>%
ggplot(aes(x = ciq_lower, y = estimate_p)) +
geom_line(size = 1.3) +
geom_line(aes(x = ciq_upper, y = estimate_p), size = 1.3) +
geom_line(aes(x = estimate_q, y = estimate_p), linetype = 2) +
geom_ribbon(aes(xmin = ciq_lower, xmax = ciq_upper), alpha = .1, fill = "purple") +
geom_point(data = lower_conf_fcn(tbl, percentile = percentile), aes(estimate_q, estimate_p), color = "purple", size = 2) +
geom_label_repel(
data = lower_conf_fcn(tbl, percentile = percentile),
aes(estimate_q, estimate_p),
label = str_glue("1-sided, 95% Confidence Bound:\n{lower_conf_fcn(rileysim_conf_tbl, percentile = .1) %>% pluck(1)} {units}"),
fill = "#8bd646ff",
color = "black",
segment.color = "black",
segment.size = .5,
nudge_y = .13,
nudge_x = -25
) +
geom_segment(data = tbl %>%
filter(estimate_p == percentile), aes(x = ciq_lower, xend = ciq_upper, y = estimate_p, yend = estimate_p), linetype = 3) +
theme_bw() +
labs(
x = "Stress (MPa)",
y = "Percentile",
caption = "Dotted line is estimate of failure strength distribution\nConfidence bands are 2-sided 90% (i.e. 1-sided 95 for lower)",
title = "Sensitivity Testing of Stent Durability",
subtitle = str_glue("placeholder")
)
}
a <- plot_cdf_fcn(tbl = rileysim_conf_tbl, percentile = .1)
a +
labs(subtitle = str_glue("Estimates: Mean = {muhat %>% round(1)} MPa, Sigma = {sighat %>% round(1)} MPa"))
Normal Probability Plot
Engineers in my industry have an unhealthy obsession to normal probability plots. Personally I don’t like them, but Minitab presents them by default and engineers in my industry will look for data in this format. As part of this project I taught myself how to convert distributional data from a CFD into a normal probability plot. I show the helper function here and the result.
norm_probability_plt_fcn <- function(tbl, percentile, units = "MPa") {
conf_tbl <- tbl %>%
mutate(qprobs = qnorm(estimate_p)) %>%
arrange(qprobs)
probs_of_interest <- c(0.01, 0.05, seq(0.1, 0.9, by = 0.1), 0.95, 0.99)
probs_of_interest_tbl <- conf_tbl %>%
filter(estimate_p %in% probs_of_interest)
conf_tbl %>%
ggplot() +
geom_line(aes(x = ciq_lower, y = qprobs), size = 1.3) +
geom_line(aes(x = ciq_upper, y = qprobs), size = 1.3) +
geom_line(aes(x = estimate_q, y = qprobs), linetype = 2) +
geom_ribbon(aes(xmin = ciq_lower, xmax = ciq_upper, y = qprobs), alpha = .1, fill = "purple") +
geom_point(data = lower_conf_fcn(tbl, percentile = percentile), aes(estimate_q, qprobs), color = "purple", size = 2) +
geom_label_repel(
data = lower_conf_fcn(tbl, percentile = percentile),
aes(estimate_q, qprobs),
label = str_glue("1-sided, 95% Confidence Bound:\n{lower_conf_fcn(rileysim_conf_tbl, percentile = .1) %>% pluck(1)} {units}"),
fill = "#8bd646ff",
color = "black",
segment.color = "black",
segment.size = .5,
nudge_y = 1,
nudge_x = -20
) +
geom_segment(data = conf_tbl %>%
filter(estimate_p == percentile), aes(x = ciq_lower, xend = ciq_upper, y = qprobs, yend = qprobs), linetype = 3) +
scale_y_continuous(limits = range(conf_tbl$qprobs), breaks = probs_of_interest_tbl$qprobs, labels = 100 * probs_of_interest_tbl$estimate_p) +
theme_bw() +
labs(
x = "Stress (MPa)",
y = "Percentile",
caption = "Dotted line is estimate of failure strength distribution\nConfidence bands are 2-sided 90%",
title = "Sensitivity Testing of Stent Durability",
subtitle = str_glue("TBD_2")
)
}
b <- norm_probability_plt_fcn(rileysim_conf_tbl, percentile = .1)
b +
labs(subtitle = str_glue("Estimates: Mean = {muhat %>% round(1)} MPa, Sigma = {sighat %>% round(1)} MPa"))
Conclusion and Thanks
There you have it! A way to determine failure strength distributions using principled, sequential testing techniques guided by gonogo. If you’ve made it this far I really appreciate your attention. I would like to thank Paul Roediger for producing this amazing toolkit and for graciously offering your time to help me troubleshoot and work through some challenges on this project earlier this year. I’ll always be grateful to the open source community for making these things possible.
Session Info
sessionInfo()## R version 4.0.3 (2020-10-10)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 18363)
##
## Matrix products: default
##
## locale:
## [1] LC_COLLATE=English_United States.1252
## [2] LC_CTYPE=English_United States.1252
## [3] LC_MONETARY=English_United States.1252
## [4] LC_NUMERIC=C
## [5] LC_TIME=English_United States.1252
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] ggalt_0.4.0 gonogo_0.1.0 here_1.0.0 ggrepel_0.8.2
## [5] plotly_4.9.2.1 gt_0.2.2 forcats_0.5.0 stringr_1.4.0
## [9] dplyr_1.0.7 purrr_0.3.4 readr_1.4.0 tidyr_1.1.3
## [13] tibble_3.1.4 ggplot2_3.3.5 tidyverse_1.3.0
##
## loaded via a namespace (and not attached):
## [1] fs_1.5.0 lubridate_1.7.9.2 ash_1.0-15 RColorBrewer_1.1-2
## [5] httr_1.4.2 rprojroot_2.0.2 tools_4.0.3 backports_1.2.0
## [9] bslib_0.3.0 utf8_1.2.2 R6_2.5.1 KernSmooth_2.23-18
## [13] DBI_1.1.0 lazyeval_0.2.2 colorspace_2.0-2 withr_2.4.2
## [17] tidyselect_1.1.1 compiler_4.0.3 extrafontdb_1.0 cli_3.0.1
## [21] rvest_0.3.6 xml2_1.3.2 labeling_0.4.2 bookdown_0.21
## [25] sass_0.4.0 scales_1.1.1 checkmate_2.0.0 proj4_1.0-10
## [29] digest_0.6.28 rmarkdown_2.11 pkgconfig_2.0.3 htmltools_0.5.2
## [33] extrafont_0.17 dbplyr_2.0.0 fastmap_1.1.0 highr_0.9
## [37] maps_3.3.0 htmlwidgets_1.5.4 rlang_0.4.11 readxl_1.3.1
## [41] rstudioapi_0.13 jquerylib_0.1.4 generics_0.1.0 farver_2.1.0
## [45] jsonlite_1.7.2 magrittr_2.0.1 Rcpp_1.0.7 munsell_0.5.0
## [49] fansi_0.5.0 lifecycle_1.0.1 stringi_1.7.4 yaml_2.2.1
## [53] MASS_7.3-53 grid_4.0.3 crayon_1.4.1 haven_2.3.1
## [57] hms_0.5.3 knitr_1.34 pillar_1.6.2 reprex_0.3.0
## [61] glue_1.4.2 evaluate_0.14 blogdown_0.15 data.table_1.14.0
## [65] modelr_0.1.8 vctrs_0.3.8 Rttf2pt1_1.3.8 cellranger_1.1.0
## [69] gtable_0.3.0 assertthat_0.2.1 xfun_0.26 broom_0.7.8
## [73] viridisLite_0.4.0 ellipsis_0.3.2https://www.wiley.com/en-us/Statistical+Methods+for+Reliability+Data%2C+2nd+Edition-p-9781118115459↩︎
https://www2.lbl.gov/ritchie/Library/PDF/2020%20Cao-Nitinol%20HCF.pdf↩︎
Neyer provided a commercial software called Sentest to facilitate practitioners who wanted to use D-optimal methods without developing their own software↩︎
Since we only care about a 1-sided confidence interval, the 1-sided confidence bound on a specified quantile becomes analogous to a tolerance interval↩︎