When testing is costly or resource intensive, it’s not uncommon for management to ask an engineer “what are the chances that we pass?”. The answer will depend on the team’s collection of domain knowledge around the product and requirement but also in how the question is interpreted. It will also be sensitive to sample size considerations. In this post, I will show how to conduct an analysis to inform the response from both a Frequentist and Bayesian perspective. Simulation will be used whenever possible to avoid the need for external references and the predictions will be used to inform a recommendation of sample size.
- Libraries
- Background and Requirements
- Assumptions and Plan
- Predicate Data
- Frequentist
- Bayesian
- Aggregate Probability of Passing by Sample Size
- SessionInfo
Libraries
library(tidyverse)
library(tolerance)
library(patchwork)
library(ggrepel)
library(gt)
library(ggExtra)
library(brms)
library(here)Background and Requirements
We need some sort of performance test for this toy problem so let’s consider pitting corrosion resistance. Specifically, we are interested in data generated during cyclic potentiodynamic polarization (CPP) testing of a nitinol stent. The data is expressed as the difference between the breakdown potential Eb the rest potential Er, both relative to a reference electrode. The magnitude of this difference corresponds to the expected corrosion resistance in the body with larger values being better.1
Assumptions and Plan
We’ll assume that our device has 1-sided, lower spec limit of +300 mV as a requirement. We’ll also assume that based on our risk analysis procedure, pitting corrosion falls in a zone mandating that at least 90% of the population will meet the requirement with 90% confidence. Thus, we need to use our test data to create a 1-sided, 90/90 tolerance interval to compare against the requirements. If you are unfamiliar with tolerance intervals, refer to this older post of mine. We’ll also assume that the default sample size would be n=9, chosen somewhat arbitrarily (we’ll consider other sample sizes later on).
Predicate Data
We would never go into any late-stage testing without some directional data from pilot studies or predicate devices. These data are usually sparse and they come with caveats, but they inform the range or possible expectations. In this example, let’s assume we have n=3 data points from early feasibility testing of a early prototype for our product. We’ll throw them into a table and then quickly check some summary stats. From testing other products and reviewing literature, we also know that the population of Eb - Er data for a particular configuration tend to be normally distributed.
legacy_data_tbl <- tibble(eb_minus_er = c(424, 543, 571))
sum_data <- legacy_data_tbl %>%
summarize(mean = mean(eb_minus_er),
sd = sd(eb_minus_er)) %>%
mutate(across(is.numeric, round, digits = 1))
sum_data %>%
gt_preview()| mean | sd | |
|---|---|---|
| 1 | 512.7 | 78.1 |
Frequentist
Simulated experiments with a single set of assumed parameters
For the Frequentist simulation, our plan is to specify the parameters of the assumed population and then repeat a simulated experiment may times. For each rep of the sim we assess the resultant tolerance limit against the requirement. This tells us the long-run frequency (interpreted as probability in the frequentist framework) of passing the test based on our experimental setup and the assumed parameters. Later on, we can adjust the sample size or the assumed population parameters to see how our chance of passing is affected.
Let’s do 1 full simulation using a sample size of n=9 and a mean and sd taken from our predicate data shown above.
Simulate the Data
reps <- 1000
set.seed(127)
n <- 9
single_sim_tbl <-
tibble(
n = n,
mean = sum_data$mean, #mean from predicate data
sd = sum_data$sd) %>% #ds from predicate data
slice(rep(1:n(), each = reps)) %>%
mutate(replicate = seq(from = 1, to = reps)) %>%
mutate(sim_data = pmap(.l = list(n = n, mean = mean, sd = sd), .f = rnorm)) %>% #create the random data points, n=9 per sim
unnest() %>%
group_by(mean, sd, replicate) %>%
summarize(ltl = normtol.int(sim_data, P = .9, alpha = .1)) %>% #calculate 90/90 tolerance interval
unnest() %>%
ungroup() %>%
rename(ltl = "1-sided.lower") %>%
select(1:7) %>%
mutate(fail = case_when(
ltl <= 300 ~ 1,
TRUE ~ 0)) %>% #flag failures
mutate(across(c(x.bar, ltl), round, digits = 1))
single_sim_tbl %>%
gt_preview()| mean | sd | replicate | alpha | P | x.bar | ltl | fail | |
|---|---|---|---|---|---|---|---|---|
| 1 | 512.7 | 78.1 | 1 | 0.1 | 0.9 | 522.5 | 410.0 | 0 |
| 2 | 512.7 | 78.1 | 2 | 0.1 | 0.9 | 515.5 | 437.0 | 0 |
| 3 | 512.7 | 78.1 | 3 | 0.1 | 0.9 | 480.4 | 283.1 | 1 |
| 4 | 512.7 | 78.1 | 4 | 0.1 | 0.9 | 518.1 | 315.8 | 0 |
| 5 | 512.7 | 78.1 | 5 | 0.1 | 0.9 | 510.8 | 353.5 | 0 |
| 6..999 | ||||||||
| 1000 | 512.7 | 78.1 | 1000 | 0.1 | 0.9 | 493.9 | 286.8 | 1 |
Calculate Frequency of Success
Having generated and stored the above simulation, it is straightforward to calculate the predicted success rate. We see that the long run frequency of success is 84%, conditional on all of our strict assumptions about population parameters and fixed sample size:
single_sim_tbl %>%
summarize(total_simulated_experiments = n(),
sum_pass = n() - sum(fail)) %>%
mutate(prop_pass = sum_pass/total_simulated_experiments) %>%
gt_preview()| total_simulated_experiments | sum_pass | prop_pass | |
|---|---|---|---|
| 1 | 1000 | 844 | 0.844 |
Visualize
Here we look at the means and lower tolerance limits (LTLs) from the simulation to help us gut check the conclusions and further understand what is going on.
single_sim_tbl %>%
pivot_longer(cols = c(x.bar, ltl), names_to = "param", values_to = "value") %>%
mutate(param = case_when(param == "x.bar" ~ "mean",
TRUE ~ "lower_tolerance_limit")) %>%
ggplot(aes(x = param, y = value)) +
geom_line(aes(group = replicate), size = .1, alpha = .1) +
geom_jitter(aes(color = param), size = .4, alpha = .4, width = .01) +
geom_hline(yintercept = 300, color = "firebrick", linetype = 2) +
theme_classic() +
theme(legend.title=element_blank()) +
labs(title = "Means and Lower Tolerance Limits for 1000 Simulated Experiments",
subtitle = "Each sim: n=9 data points draws from a normal distribution",
x = "",
y = "Eb - Er [mV SCE]",
caption = "red dotted line indicates lower spec limit")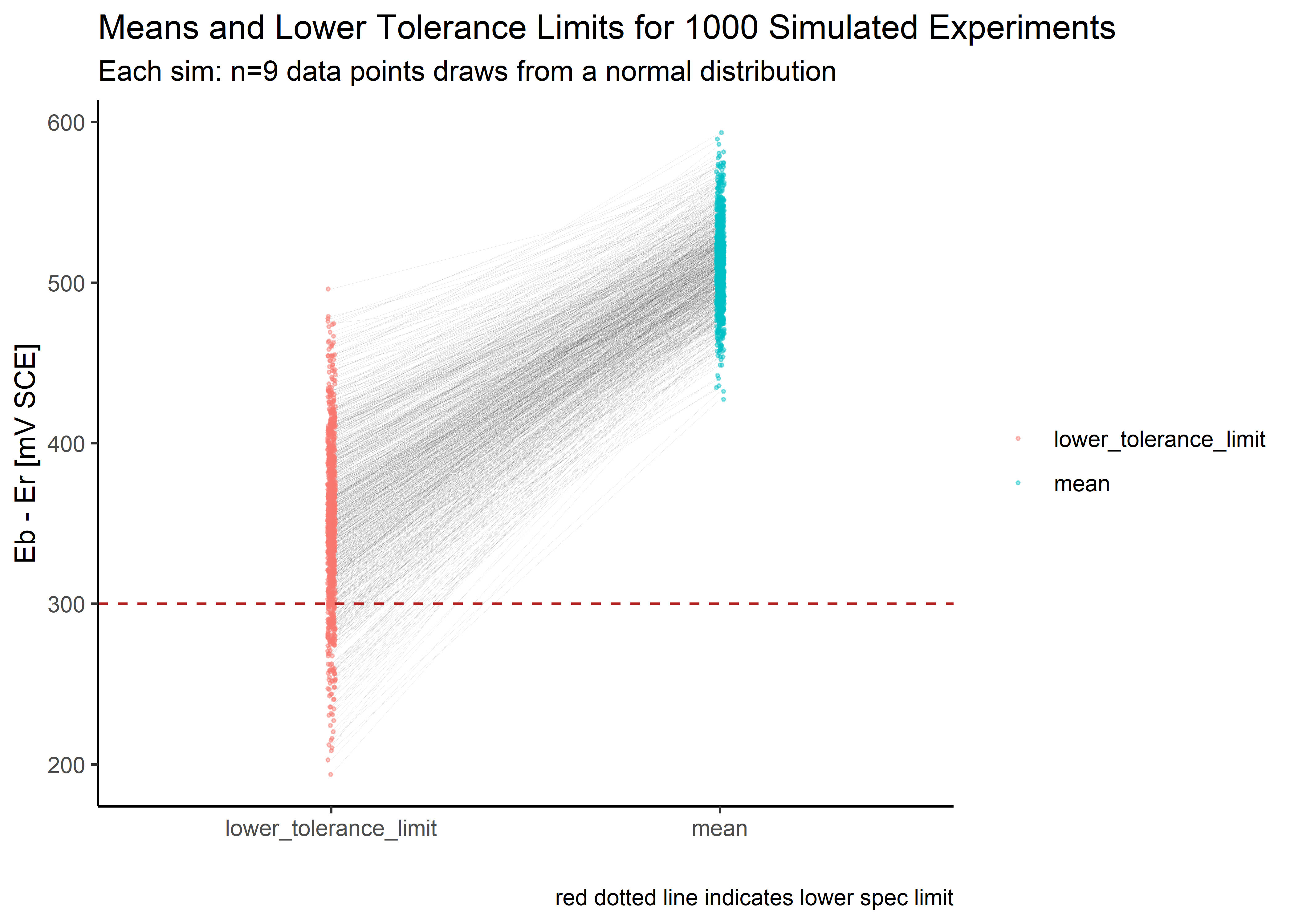
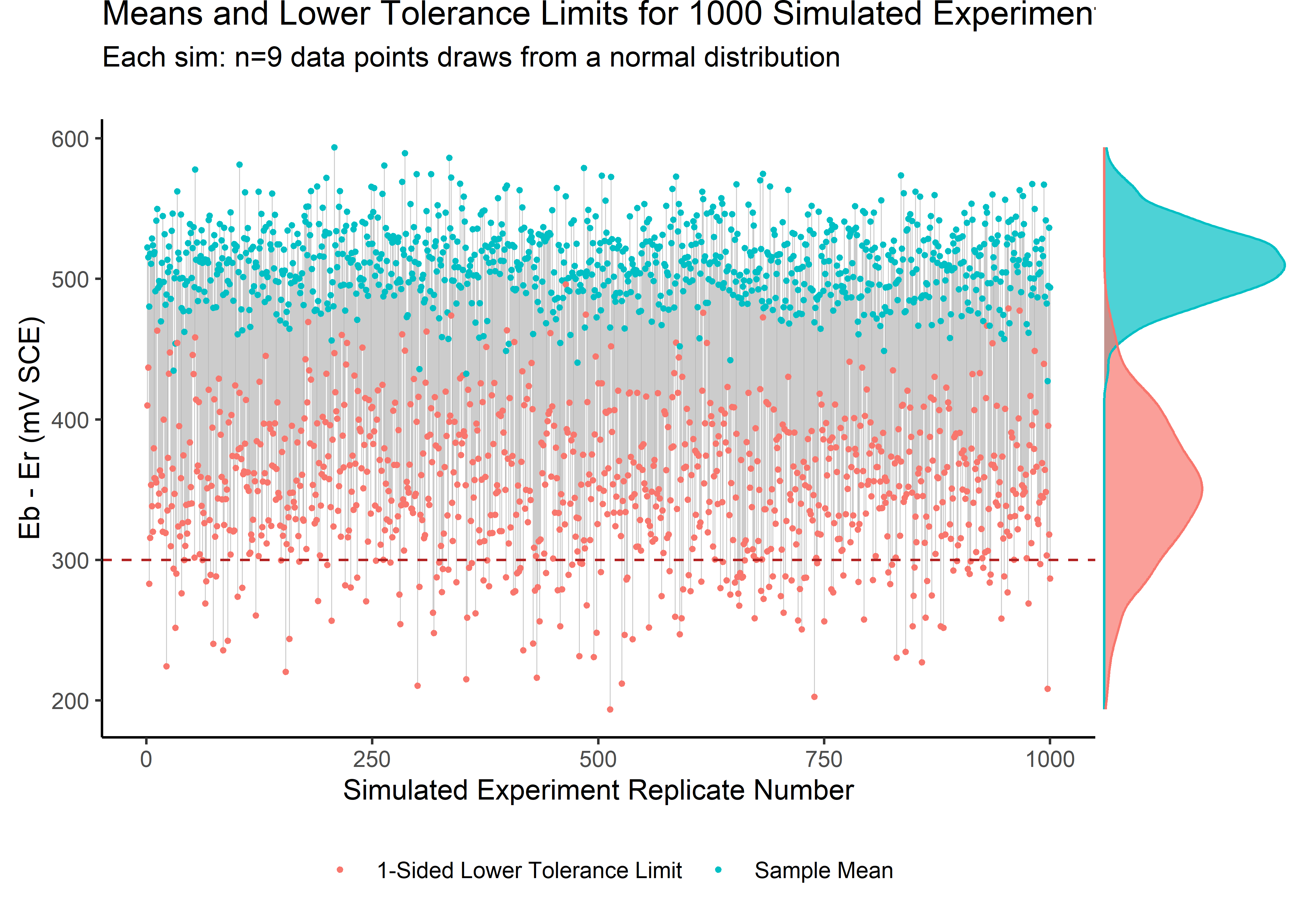
And here we look by simulation run number and add the marginal distributions for mean and sd.
int_plot <- single_sim_tbl %>%
ggplot(aes(group = replicate)) +
geom_segment(aes(x = replicate, y = x.bar, xend = replicate, yend = ltl), size = .2, alpha = .2) +
geom_point(data = single_sim_tbl %>%
pivot_longer(cols = c(x.bar, ltl), names_to = "param", values_to = "value") %>%
mutate(param = case_when(param == "x.bar" ~ "Sample Mean", TRUE ~ "1-Sided Lower Tolerance Limit")),
aes(x = replicate, y = value, color = param), size = .6) +
geom_hline(yintercept = 300, linetype = 2, color = "firebrick") +
theme_classic() +
theme(legend.position = "bottom") +
labs(y = "Eb - Er (mV SCE)",
x = "Simulated Experiment Replicate Number",
title = "Means and Lower Tolerance Limits for 1000 Simulated Experiments",
subtitle = "Each sim: n=9 data points draws from a normal distribution") +
theme(legend.title=element_blank())
ggMarginal(int_plot,
groupColour = TRUE,
groupFill = TRUE,
type = "density",
alpha = 0.7,
margins = "y"
)
Nested Simulation with Many Sets of Parameters
The simulation above makes strict assumptions about the population parameters and uses only a single fixed sample size. we know intuitively that there is lot-to-lot variability and we have our choice of sample size, within reason, when we proceed with our eventual real-world test. Thus, what we really want to understand is the probability of success for a wide range of parameter assumptions and sample sizes. For that, we’ll need a more complex simulation.
In the code below, a grid of possibilities is explored for potential values of mean, sd, and sample size. Each permutation is a nested simulation of n=1000. Ranges explored (the range for mean goes mostly lower and the range for sd goes mostly higher as we really want to understand what happens if our predicate data was overly optimistic):
- mean: 300 to 500 mV
- sd: 75 to 179 mV
- n: 5 to 17 parts
Simulated the Data
The workflow below is very similar to the single simulation section with a few exceptions. The expand_grid() function is what generated all combinations of the specified sequences for mean, sd, and n. slice() is used to copy and append rows, and a “scenario” column is added to track each permutation of the 3 variables.
set.seed(2015)
reps <- 1000
mean = c(seq(from = 300, to = 500, by = 50), sum_data$mean)
sd = c(seq(from = 75, to = 175, by = 25), sum_data$sd)
n = seq(from = 5, to = 17, by = 2)
full_even_sim_tbl <- expand_grid(mean, sd, n) %>%
mutate(mean = mean %>% round(0),
sd = sd %>% round(0)) %>%
mutate(scenario = seq(from = 1, to = nrow(.))) %>%
slice(rep(1:n(), each = reps)) %>%
mutate(replicate_number = rep(seq(from = 1, to = reps), nrow(.)/reps)) %>%
mutate(sim_data = pmap(.l = list(n = n, mean = mean, sd=sd), .f = rnorm)) %>%
unnest(cols = everything()) %>%
group_by(mean, sd, scenario, replicate_number, n) %>%
summarize(ltl = normtol.int(sim_data, P = .9, alpha = .1)) %>%
unnest(cols = everything()) %>%
ungroup() %>%
rename(ltl = '1-sided.lower',
utl = '1-sided.upper') %>%
mutate(fail = case_when(ltl <= 300 ~ 1,
TRUE ~ 0))
full_even_sim_tbl %>%
mutate(across(c(x.bar, ltl, utl), round, digits = 1)) %>%
gt_preview()| mean | sd | scenario | replicate_number | n | alpha | P | x.bar | ltl | utl | fail | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 300 | 75 | 1 | 1 | 5 | 0.1 | 0.9 | 258.4 | 97.0 | 419.8 | 1 |
| 2 | 300 | 75 | 1 | 2 | 5 | 0.1 | 0.9 | 294.2 | 58.8 | 529.6 | 1 |
| 3 | 300 | 75 | 1 | 3 | 5 | 0.1 | 0.9 | 323.1 | 172.7 | 473.4 | 1 |
| 4 | 300 | 75 | 1 | 4 | 5 | 0.1 | 0.9 | 270.5 | 90.4 | 450.6 | 1 |
| 5 | 300 | 75 | 1 | 5 | 5 | 0.1 | 0.9 | 302.1 | 231.9 | 372.2 | 1 |
| 6..251999 | |||||||||||
| 252000 | 513 | 175 | 245 | 1000 | 17 | 0.1 | 0.9 | 532.5 | 191.6 | 873.4 | 1 |
Calculate Frequency of Success
Now, each scenario (combination of assumed mean, sd, and sample size) has its own probability (long run frequency) of passing:
summary_tbl <- full_even_sim_tbl %>%
group_by(mean, sd, n, max(replicate_number)) %>%
summarize(number_fail = sum(fail)) %>%
rename(reps = 'max(replicate_number)') %>%
mutate(avg = stringr::str_glue("mean Eb-Er = {as_factor(mean)} mV [SCE]")) %>%
mutate(prop_pass = 1-(number_fail / reps)) %>%
ungroup()
summary_tbl %>%
gt_preview()| mean | sd | n | reps | number_fail | avg | prop_pass | |
|---|---|---|---|---|---|---|---|
| 1 | 300 | 75 | 5 | 1000 | 997 | mean Eb-Er = 300 mV [SCE] | 0.003 |
| 2 | 300 | 75 | 7 | 1000 | 1000 | mean Eb-Er = 300 mV [SCE] | 0.000 |
| 3 | 300 | 75 | 9 | 1000 | 1000 | mean Eb-Er = 300 mV [SCE] | 0.000 |
| 4 | 300 | 75 | 11 | 1000 | 1000 | mean Eb-Er = 300 mV [SCE] | 0.000 |
| 5 | 300 | 75 | 13 | 1000 | 1000 | mean Eb-Er = 300 mV [SCE] | 0.000 |
| 6..251 | |||||||
| 252 | 513 | 175 | 17 | 1000 | 938 | mean Eb-Er = 513 mV [SCE] | 0.062 |
Visualize - Power Curves
Plotting these data produce so-called power curves from which we can easily see trends for probability of passing based on the parameter assumptions and our choice of sample size. Constructing these curves provide a principled way to select a reasonable sample size.
summary_tbl %>%
ggplot(aes(x = sd, y = prop_pass)) +
geom_point(aes(color = as_factor(n))) +
geom_line(aes(color = as_factor(n))) +
geom_vline(xintercept = sum_data$sd, color = "firebrick", linetype = 2) +
facet_wrap(~ avg) +
lims(x = c(75, 175)) +
scale_color_discrete(name = "Sample Size") +
#scale_color_viridis_d(option = "C", end = .8) +
labs(x = "Standard Deviation (mV [SCE])",
y = str_glue("Passing Proportion\nBased on n={reps} simulations each")) +
theme_bw() +
labs(title = "Predicted Power Curves for Simulated Corrosion Experiments",
subtitle = "as a function of mean, standard deviation, and sample size",
caption = "513 mV facet represents predicate mean, red dotted line represents predicate sd")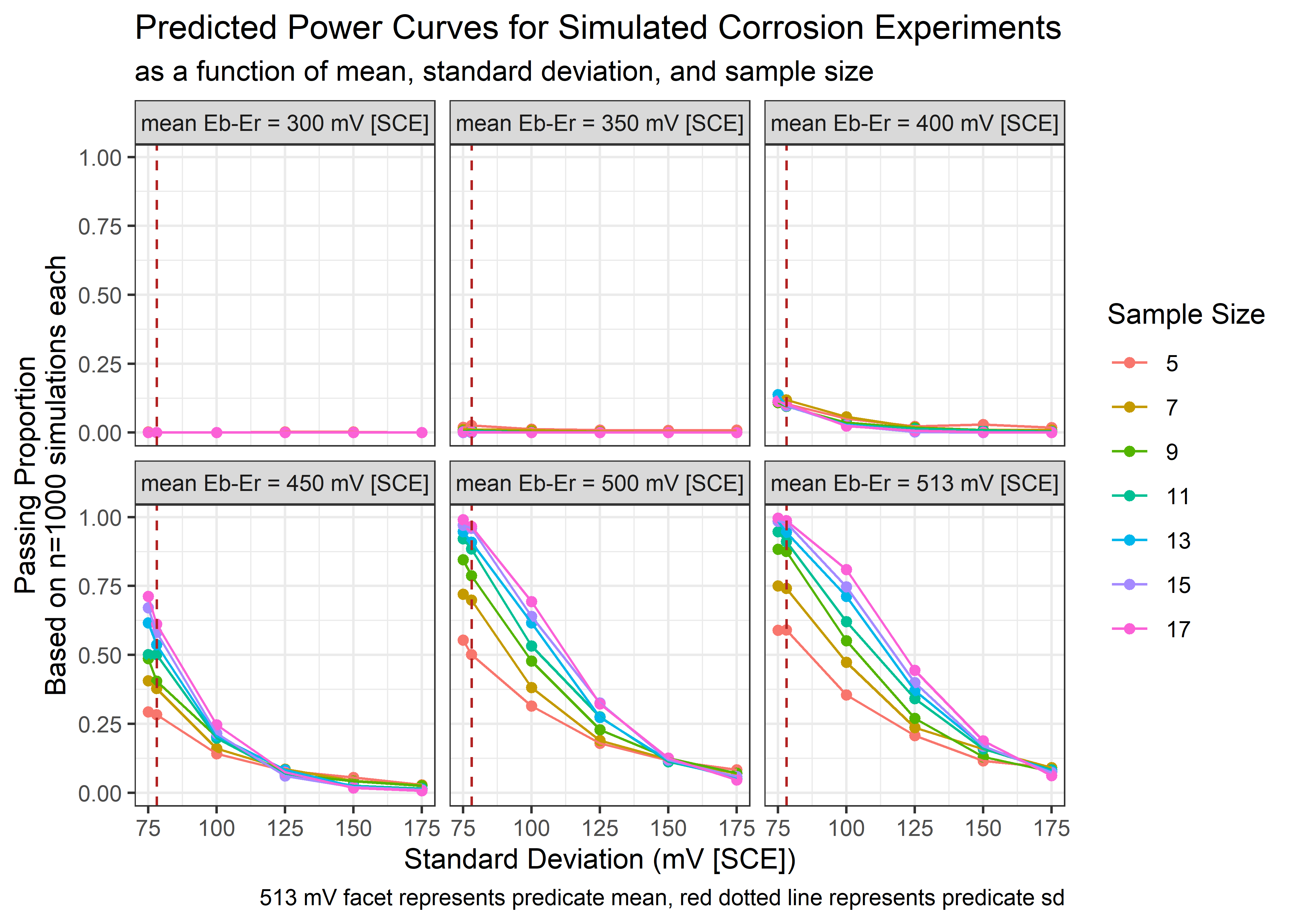 We note that at the lower means and higher sds we would have very low chance of passing.
We note that at the lower means and higher sds we would have very low chance of passing.
Bayesian
As engineers, we can look through the range of possible inputs and think about how plausible they might be based on our understanding of the product and domain. But there is no formal way to leverage that knowledge in the frequentist framework. For that, we need a Bayesian approach.
Priors
In the code below, we want to ask ourselves what values are reasonable for the parameters of interest. We happen to know from other devices and literature that the mean tends to fall in the 200-800 range. We select a t distribution on this parameter centered at 500 with a few degrees of freedom. This is conservative since it spreads our “belief” wider than a normal distribution, including more options in the tails. For the sd, we apply a uniform distribution over a generous range, making sure to keep all values positive.
Specify Priors
We put these into this table form because we’ll want to plot these curves to confirm visually that our assumptions make sense.
prior_pred_tbl <- tibble(
mu = rstudent_t(n = 300, df = 3, mu = 500, sigma = 100),
sig = runif(300, min = 20, max = 200) %>% abs()
) %>%
mutate(row_id = row_number()) %>%
select(row_id, everything()) %>%
mutate(plotted_y_data = map2(mu, sig, ~ tibble(
x = seq(-200, 1000, length.out = 10000),
y = dnorm(x, .x, .y)
))) %>%
# slice(1) %>%
unnest() %>%
mutate(model = "mu ~ student(3, 500, 100), sigma ~ unif(20,200)")
prior_pred_tbl %>%
gt_preview()| row_id | mu | sig | x | y | model | |
|---|---|---|---|---|---|---|
| 1 | 1 | 399.9662 | 134.5556 | -200.00 | 1.428195e-07 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
| 2 | 1 | 399.9662 | 134.5556 | -199.88 | 1.433886e-07 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
| 3 | 1 | 399.9662 | 134.5556 | -199.76 | 1.439598e-07 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
| 4 | 1 | 399.9662 | 134.5556 | -199.64 | 1.445331e-07 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
| 5 | 1 | 399.9662 | 134.5556 | -199.52 | 1.451087e-07 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
| 6..2999999 | ||||||
| 3000000 | 300 | 585.2949 | 29.1041 | 1000.00 | 1.118222e-46 | mu ~ student(3, 500, 100), sigma ~ unif(20,200) |
Visualize Prior Pred
This vis shows a variety of possible outcomes for Eb-Er before seeing the data.
prior_pred_tbl %>%
ggplot(aes(x = x, y = y, group = row_id)) +
geom_line(aes(x, y), size = .5, alpha = .2, color = "#2c3e50") +
labs(
x = "mV [SCE]",
y = "",
title = "Prior Predictive Simulations"
) +
theme_minimal() + theme(
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
Data
Specify Data
We re-enter our legacy data.
p_tbl <- tibble(p = c(424, 543, 571))Likelihood and Model Fitting
Fit Model with brms
Having specified our data and priors, we can assume a likelihood and brms can do the rest. Here we assume Gaussian (normal) for the likelihood of the data and copy our priors from the previous section. Once fit, we’ll have access to a posterior in table form comprised of credible values for the mean and sd for many possible normal distributions. This is similar to the grid of values we build manually in the frequentist section to generate power curve, but now now they are weighted by plausibility.
pa_mod_1 <-
brm(
data = p_tbl, family = gaussian,
p ~ 1,
prior = c(
prior(student_t(3, 500, 100), class = Intercept),
prior(uniform(1, 200), class = sigma)),
iter = 41000, warmup = 40000, chains = 4, cores = 4,
seed = 4
)
summary(pa_mod_1)## Family: gaussian
## Links: mu = identity; sigma = identity
## Formula: p ~ 1
## Data: p_tbl (Number of observations: 3)
## Draws: 4 chains, each with iter = 41000; warmup = 40000; thin = 1;
## total post-warmup draws = 4000
##
## Population-Level Effects:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## Intercept 508.58 50.22 402.45 608.44 1.00 1314 988
##
## Family Specific Parameters:
## Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
## sigma 105.34 40.47 44.68 190.13 1.00 1198 1360
##
## Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
## and Tail_ESS are effective sample size measures, and Rhat is the potential
## scale reduction factor on split chains (at convergence, Rhat = 1).Visualize Chains and Posterior
This section provided diagnostic plots for the Markov Chain Monte Carlo. Chains look well dispersed and relatively similar (good) with a “fuzzy caterpillar” look that we want.
plot(pa_mod_1)
Examine Posterior Draws
Let’s take a peek at the table of samples from the posterior. They look reasonable.
pa_mod_1_post_tbl <- posterior_samples(pa_mod_1) %>%
select(-lp__) %>%
rename("mu" = b_Intercept)
pa_mod_1_post_tbl %>%
gt_preview()| mu | sigma | |
|---|---|---|
| 1 | 474.3346 | 124.91147 |
| 2 | 570.3584 | 102.00744 |
| 3 | 625.1128 | 98.52465 |
| 4 | 598.0249 | 110.21080 |
| 5 | 521.2838 | 88.29519 |
| 6..3999 | ||
| 4000 | 593.9553 | 87.95511 |
Use Posterior to Estimate Probability of Passing with Various Sample Sizes
Now that we have the posterior, we can repeat a series of simulations using parameters from each row of the sampled posterior. This will preserve the uncertainty captured in the posterior and allow us to estimate the probability of passing, weighted by our beliefs and the informed by the data.
Simulate the Data
Knowing that the posterior draws represent credible values population mean and sd, our goal is to produce a new simulation that conducts and a simulated experiment over every credible combination. This is very similar to our frequentist version above, but instead of just copying arbitrary combinations of parameters over a grid, here the posterior draws have already selected credible values for the parameters. This is sort of like a “weighted” version of the frequentist simulation that is compatible with our pre-existing beliefs as established by the priors and then updated though the predicate data.
set.seed(2015)
reps <- 1000
n = seq(from = 5, to = 17, by = 2)
b_sim_tbl <- pa_mod_1_post_tbl %>%
rename(mean = mu,
sd = sigma) %>%
mutate(scenario = seq(from = 1, to = nrow(.))) %>%
slice(rep(1:n(), each = length(n))) %>%
mutate(num_draws = rep(x = n, times = nrow(.)/length(n))) %>%
mutate(dat = pmap(.l = list(n = num_draws, mean = mean, sd=sd), .f = rnorm)) %>%
unnest(cols = everything()) %>%
group_by(mean, sd, scenario, num_draws) %>%
summarize(ltl = normtol.int(dat, P = .9, alpha = .1)) %>%
unnest(cols = everything()) %>%
ungroup() %>%
arrange(scenario) %>%
rename(ltl = '1-sided.lower',
utl = '1-sided.upper') %>%
mutate(fail = case_when(ltl <= 300 ~ 1,
TRUE ~ 0)) %>%
select(-utl) %>%
mutate(across(is.numeric, round, digits = 1))
b_sim_tbl %>%
gt_preview()| mean | sd | scenario | num_draws | alpha | P | x.bar | ltl | fail | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 474.3 | 124.9 | 1 | 5 | 0.1 | 0.9 | 405.1 | 136.3 | 1 |
| 2 | 474.3 | 124.9 | 1 | 7 | 0.1 | 0.9 | 462.0 | 168.3 | 1 |
| 3 | 474.3 | 124.9 | 1 | 9 | 0.1 | 0.9 | 466.8 | 241.9 | 1 |
| 4 | 474.3 | 124.9 | 1 | 11 | 0.1 | 0.9 | 493.6 | 183.8 | 1 |
| 5 | 474.3 | 124.9 | 1 | 13 | 0.1 | 0.9 | 477.1 | 224.4 | 1 |
| 6..27999 | |||||||||
| 28000 | 594.0 | 88.0 | 4000 | 17 | 0.1 | 0.9 | 541.4 | 392.9 | 0 |
Aggregate Probability of Passing by Sample Size
Count the number of simulations that pass/fail at each sample size condition:
agg_tbl <- b_sim_tbl %>%
group_by(num_draws) %>%
summarize(total_fail = sum(fail),
total_trials = 4000) %>%
ungroup() %>%
rename(sample_size = num_draws) %>%
mutate(prob_passing = 1-(total_fail / total_trials)) %>%
mutate(prob_passing = scales::percent(prob_passing, accuracy = 1))
agg_tbl %>%
select(sample_size, prob_passing) %>%
gt()| sample_size | prob_passing |
|---|---|
| 5 | 42% |
| 7 | 51% |
| 9 | 54% |
| 11 | 58% |
| 13 | 60% |
| 15 | 63% |
| 17 | 63% |
Based on this estimate, the increase in probability of passing by going from, for example, n=9 to n=13 is 6% which does not seem significant enough to recommend the associated increase in cost and time for the larger sample size. However, if testing is cheap and easy, then going from, for example, n=9 to n=15 provides an estimated 9% increase in probability of passing.
The Bayesian version of the workflow has allowed us to answer the question concisely: ‘what are our chances of passing?’. The Frequentist version gives a survey of possibilities but forces you to apply your domain knowledge after the fact in an unprincipled way to arrive at a decision.
Both are useful - and I hope this post was useful to somebody too! Thank you for reading.
SessionInfo
sessionInfo()## R version 4.0.3 (2020-10-10)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 18363)
##
## Matrix products: default
##
## locale:
## [1] LC_COLLATE=English_United States.1252
## [2] LC_CTYPE=English_United States.1252
## [3] LC_MONETARY=English_United States.1252
## [4] LC_NUMERIC=C
## [5] LC_TIME=English_United States.1252
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] here_1.0.1 brms_2.16.3 Rcpp_1.0.7 ggExtra_0.9
## [5] gt_0.3.1 ggrepel_0.9.1 patchwork_1.1.1 tolerance_2.0.0
## [9] forcats_0.5.1 stringr_1.4.0 dplyr_1.0.7 purrr_0.3.4
## [13] readr_2.1.1 tidyr_1.1.4 tibble_3.1.6 ggplot2_3.3.5
## [17] tidyverse_1.3.1
##
## loaded via a namespace (and not attached):
## [1] readxl_1.3.1 backports_1.4.1 plyr_1.8.6
## [4] igraph_1.2.11 splines_4.0.3 crosstalk_1.2.0
## [7] rstantools_2.1.1 inline_0.3.19 digest_0.6.28
## [10] htmltools_0.5.2 rsconnect_0.8.25 fansi_0.5.0
## [13] magrittr_2.0.1 checkmate_2.0.0 memoise_2.0.1
## [16] tzdb_0.2.0 modelr_0.1.8 extrafont_0.17
## [19] RcppParallel_5.1.5 matrixStats_0.61.0 xts_0.12.1
## [22] extrafontdb_1.0 pkgdown_2.0.1 prettyunits_1.1.1
## [25] colorspace_2.0-2 rvest_1.0.2 haven_2.4.3
## [28] xfun_0.29 callr_3.7.0 crayon_1.4.2
## [31] jsonlite_1.7.2 lme4_1.1-27.1 zoo_1.8-9
## [34] glue_1.6.0 gtable_0.3.0 emmeans_1.7.2
## [37] V8_4.0.0 distributional_0.3.0 pkgbuild_1.3.1
## [40] Rttf2pt1_1.3.9 rstan_2.26.4 abind_1.4-5
## [43] scales_1.1.1 mvtnorm_1.1-3 DBI_1.1.2
## [46] miniUI_0.1.1.1 xtable_1.8-4 stats4_4.0.3
## [49] StanHeaders_2.26.4 DT_0.20 htmlwidgets_1.5.4
## [52] httr_1.4.2 threejs_0.3.3 posterior_1.2.0
## [55] ellipsis_0.3.2 pkgconfig_2.0.3 loo_2.4.1
## [58] farver_2.1.0 sass_0.4.0 dbplyr_2.1.1
## [61] utf8_1.2.2 labeling_0.4.2 tidyselect_1.1.1
## [64] rlang_0.4.11 reshape2_1.4.4 later_1.3.0
## [67] munsell_0.5.0 cellranger_1.1.0 tools_4.0.3
## [70] cachem_1.0.6 cli_3.1.0 generics_0.1.1
## [73] broom_0.7.11 ggridges_0.5.3 evaluate_0.14
## [76] fastmap_1.1.0 yaml_2.2.1 processx_3.5.2
## [79] knitr_1.34 fs_1.5.2 rgl_0.108.3
## [82] nlme_3.1-153 projpred_2.0.2 mime_0.12
## [85] xml2_1.3.3 compiler_4.0.3 bayesplot_1.8.1
## [88] shinythemes_1.2.0 rstudioapi_0.13 gamm4_0.2-6
## [91] curl_4.3.2 reprex_2.0.1 bslib_0.3.1
## [94] stringi_1.7.4 highr_0.9 ps_1.6.0
## [97] blogdown_0.15 Brobdingnag_1.2-6 lattice_0.20-45
## [100] Matrix_1.4-0 nloptr_1.2.2.3 markdown_1.1
## [103] shinyjs_2.1.0 tensorA_0.36.2 vctrs_0.3.8
## [106] pillar_1.6.4 lifecycle_1.0.1 jquerylib_0.1.4
## [109] bridgesampling_1.1-2 estimability_1.3 httpuv_1.6.5
## [112] R6_2.5.1 bookdown_0.21 promises_1.2.0.1
## [115] gridExtra_2.3 codetools_0.2-18 boot_1.3-28
## [118] colourpicker_1.1.1 MASS_7.3-54 gtools_3.9.2
## [121] assertthat_0.2.1 rprojroot_2.0.2 withr_2.4.3
## [124] shinystan_2.5.0 mgcv_1.8-38 parallel_4.0.3
## [127] hms_1.1.1 grid_4.0.3 minqa_1.2.4
## [130] coda_0.19-4 rmarkdown_2.11 shiny_1.7.1
## [133] lubridate_1.8.0 base64enc_0.1-3 dygraphs_1.1.1.6For additional details about this testing, refer to ASTM F2129↩︎